- Métodos
- Método de diferencias finitas en el dominio del tiempo (FDTD)
El método FDTD para la simulación electromagnética
El enfoque FDTD ofrece un excelente rendimiento de escalado del método a medida que aumenta el tamaño del problema. A medida que aumenta el número de incógnitas, el enfoque FDTD supera rápidamente a otros métodos en eficiencia.
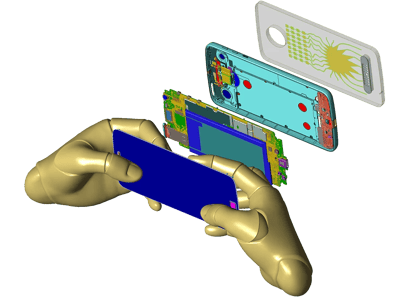
Modelo de teléfono móvil facilitado por cortesía de Motorola Mobility, LLC/Lenovo.
¿Por qué utilizar el software de simulación FDTD?
Mientras que muchas técnicas de simulación electromagnética se aplican en el dominio de la frecuencia, la FDTD resuelve las ecuaciones de Maxwell en el dominio del tiempo. Esto significa que el cálculo de los valores del campo electromagnético avanza a pasos discretos en el tiempo. Una de las ventajas del enfoque en el dominio temporal es que proporciona resultados de banda ancha a partir de una única ejecución del programa; sin embargo, la principal razón para utilizar el enfoque FDTD es el excelente rendimiento de escalado del método a medida que aumenta el tamaño del problema. A medida que aumenta el número de incógnitas, el enfoque FDTD supera rápidamente a otros métodos en eficiencia. La FDTD también se ha identificado como el método preferido para realizar simulaciones electromagnéticas de los efectos biológicos de los dispositivos inalámbricos [1]. El método FDTD ha demostrado ser el enfoque más eficiente y proporciona resultados precisos de la penetración del campo en los tejidos biológicos.
Breve resumen - Conceptos básicos de la simulación FDTD
En el enfoque FDTD, tanto el espacio como el tiempo se dividen en segmentos discretos. El espacio se segmenta en celdas con forma de caja, que son pequeñas en comparación con la longitud de onda. Los campos eléctricos se sitúan en los bordes de la caja y los magnéticos en las caras, como se muestra en la Figura 1. Esta orientación de los campos se conoce como "Y". Esta orientación de los campos se conoce como celda de Yee [2, p. 37] y es la base de la FDTD. El tiempo se cuantiza en pequeños pasos en los que cada paso representa el tiempo necesario para que el campo viaje de una celda a la siguiente. Dado el desfase en el espacio de los campos magnéticos con respecto a los campos eléctricos, los valores del campo con respecto al tiempo también están desfasados. Los campos eléctricos y magnéticos se actualizan utilizando un esquema de salto en el que primero se calculan los campos eléctricos y luego los magnéticos, a cada paso en el tiempo.
Cuando se combinan muchas celdas FDTD para formar un volumen tridimensional, el resultado es una rejilla o malla FDTD. Cada celda FDTD solapará aristas y caras con sus vecinas, por lo que, por convención, cada celda tendrá tres campos eléctricos que comienzan en un nodo común asociado a ella. Los campos eléctricos de los otros nueve bordes de la celda FDTD pertenecerán a otras celdas adyacentes. Cada celda tendrá también tres campos magnéticos originados en las caras de la celda adyacentes al nodo común de los campos eléctricos, como se muestra en la Figura 1.
Dentro de la malla, pueden añadirse materiales como conductores o dieléctricos cambiando las ecuaciones para calcular los campos en determinados lugares. Por ejemplo, para añadir un segmento de alambre perfectamente conductor a un borde de celda, la ecuación para calcular el campo eléctrico puede sustituirse simplemente por el valor cero, ya que el campo eléctrico en un conductor perfecto es idénticamente cero. Uniendo numerosos bordes de celda de extremo a extremo definidos como material perfectamente conductor, se puede formar un alambre. La introducción de otros materiales u otras configuraciones se maneja de manera similar y cada uno puede aplicarse a los campos eléctricos o magnéticos dependiendo de las características del material. Al asociar muchos bordes de celda con materiales, se puede formar una estructura geométrica dentro de la malla FDTD como la esfera dieléctrica que se muestra en la Figura 2. Cada pequeño recuadro de la figura representa una celda FDTD.
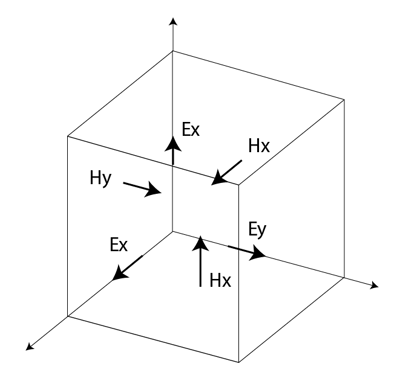
Figura 1: La célula de Yee con componentes de campo etiquetados

Figura 2: Una esfera dieléctrica mallada en una malla FDTD tradicional con escalonamiento. Los bordes de las celdas individuales (ubicaciones del campo eléctrico) se muestran como líneas de malla superpuestas.
El tamaño de la celda, las dimensiones de la caja pequeña, es la restricción más importante en cualquier simulación FDTD, ya que determina no sólo el tamaño del paso en el tiempo, sino también el límite superior de frecuencia para el cálculo. Por regla general, la resolución mínima, y por tanto el límite superior de frecuencia, es de diez celdas por longitud de onda. En la práctica, el tamaño de las celdas suele ser inferior para poder resolver las dimensiones y características de la estructura que se va a simular, como el grosor de un sustrato o la longitud de un cable.
Una excitación puede aplicarse a una simulación FDTD de muchas maneras diferentes. Un método emula la excitación de una geometría en lugares discretos aplicando una forma de onda muestreada a la ecuación de actualización del campo en uno o más lugares. En cada paso en el tiempo, el valor de la forma de onda en ese período de tiempo se añade al valor del campo. Los campos circundantes propagarán la forma de onda introducida a través de la malla FDTD de forma apropiada, dependiendo de las características de cada celda. Un cálculo debe continuar hasta que se haya alcanzado un estado de convergencia. Esto suele significar que todos los valores de campo han decaído hasta ser prácticamente cero (al menos 60 dB por debajo del pico) o que se ha alcanzado una condición de estado estacionario.
Avances en escaleras celulares
Tradicionalmente, las celdas FDTD escalonadas se consideran engorrosas e ineficaces para resolver superficies curvas o campos muy variables. Los avances en F DTD permiten crear mallas conformadas y corregir singularidades.
En general, la celda Yee de la figura 1 puede ser rectangular. Las distancias entre celdas en las direcciones x, y y z pueden variar a lo largo del espacio del problema. Esto permite colocar más bordes de celda en regiones de campos intensos, como alrededor de pequeñas características de material altamente conductor. Dentro de una celda, las ecuaciones de actualización estándar de FDTD pueden refinarse de muchas maneras, por ejemplo, para permitir cables más delgados que el tamaño de una celda o para calcular los campos intensos en los bordes de conductores como las líneas microstrip. Otro refinamiento puede permitir objetos cuya superficie intersecte la celda en ángulos arbitrarios con respecto a los ejes principales. Estas células "conformes" pueden refinarse aún más para tener en cuenta la curvatura de la superficie del objeto dentro del volumen de la célula.
La figura 3 muestra la geometría de una parte de un teléfono móvil. Para mayor claridad, se ha desactivado la visibilidad de muchas de las partes, incluida la carcasa exterior, para mostrar la región cercana a la antena. En la Figura 4a se muestra una pequeña porción de la malla FDTD del teléfono utilizando celdas rectangulares simples. En la Figura 4b se muestra la misma parte de la malla del teléfono, esta vez utilizando un tipo de tratamiento conforme para celdas que contienen porciones de la superficie de un objeto. La figura 5 muestra una vista más amplia de las superficies de la malla conformada.
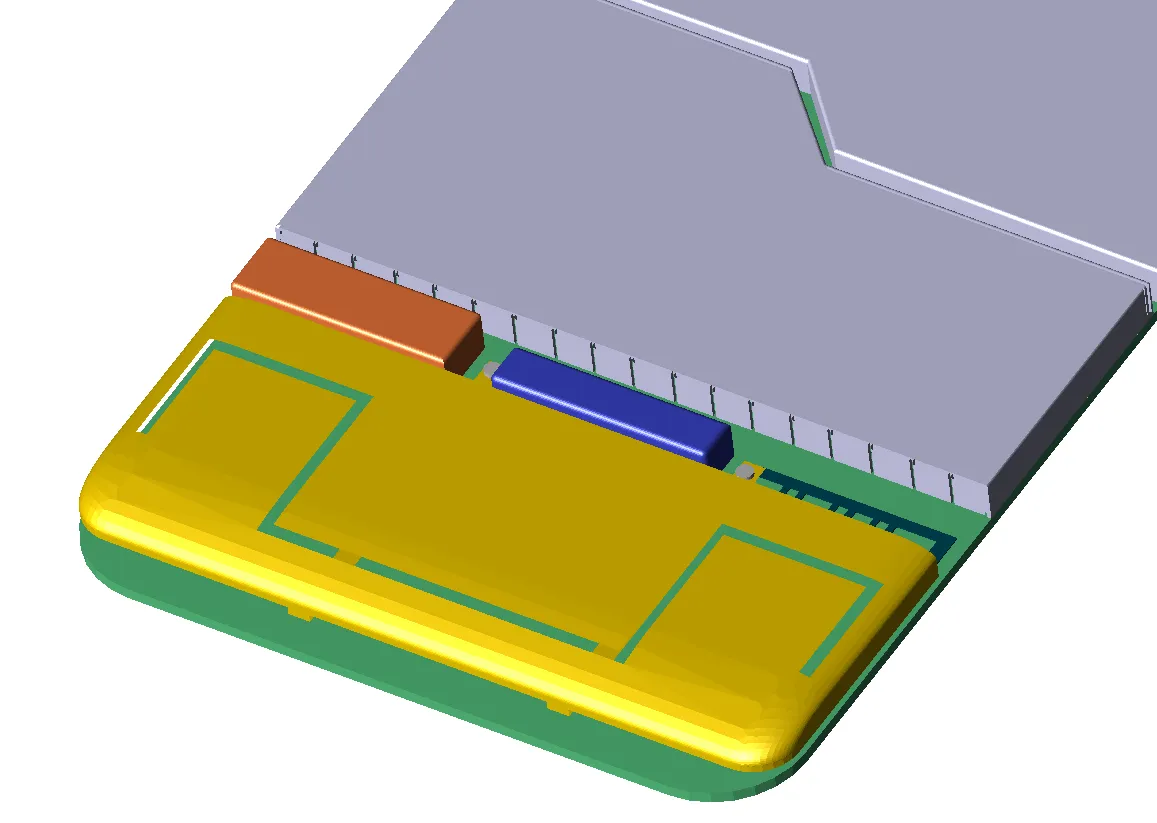
Figura 3: Sección de la antena del teléfono móvil.
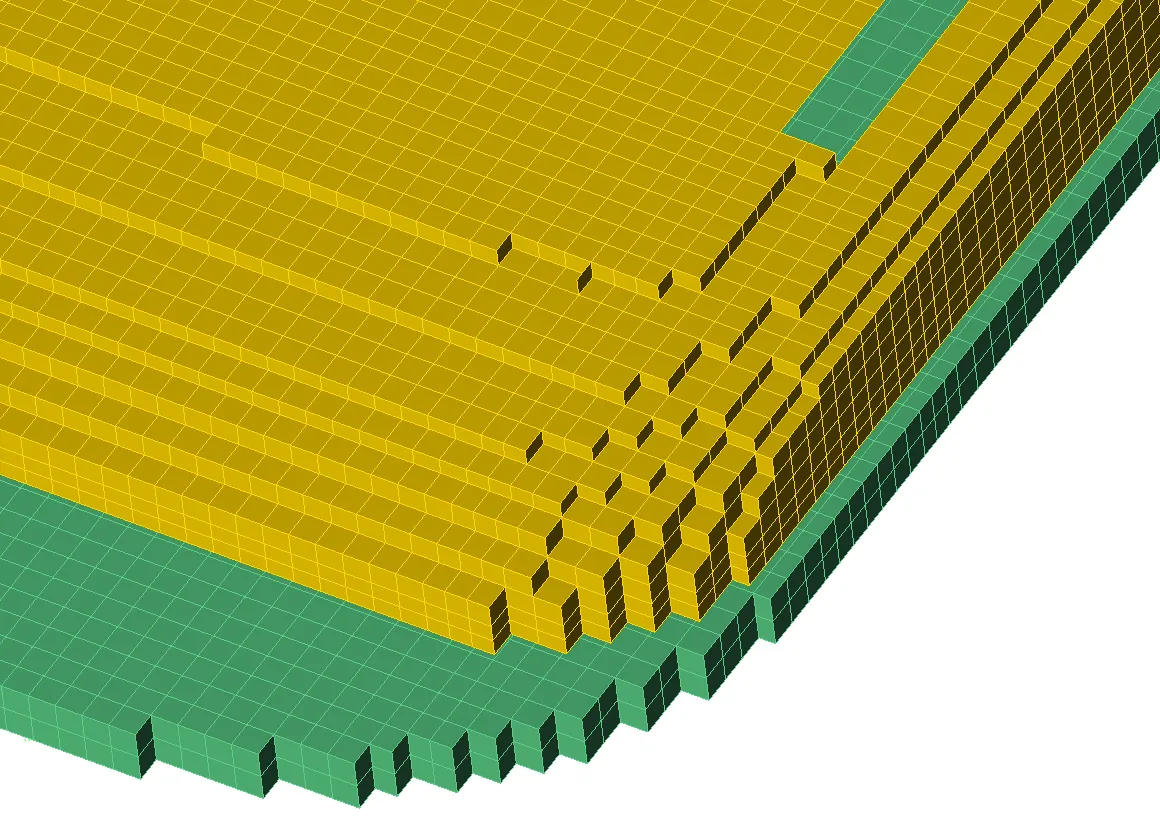
Figura 4a: Vista de malla de la esquina de la antena utilizando una malla rectangular simple.

Figura 4b: Vista de malla de la esquina de la antena con malla conforme.
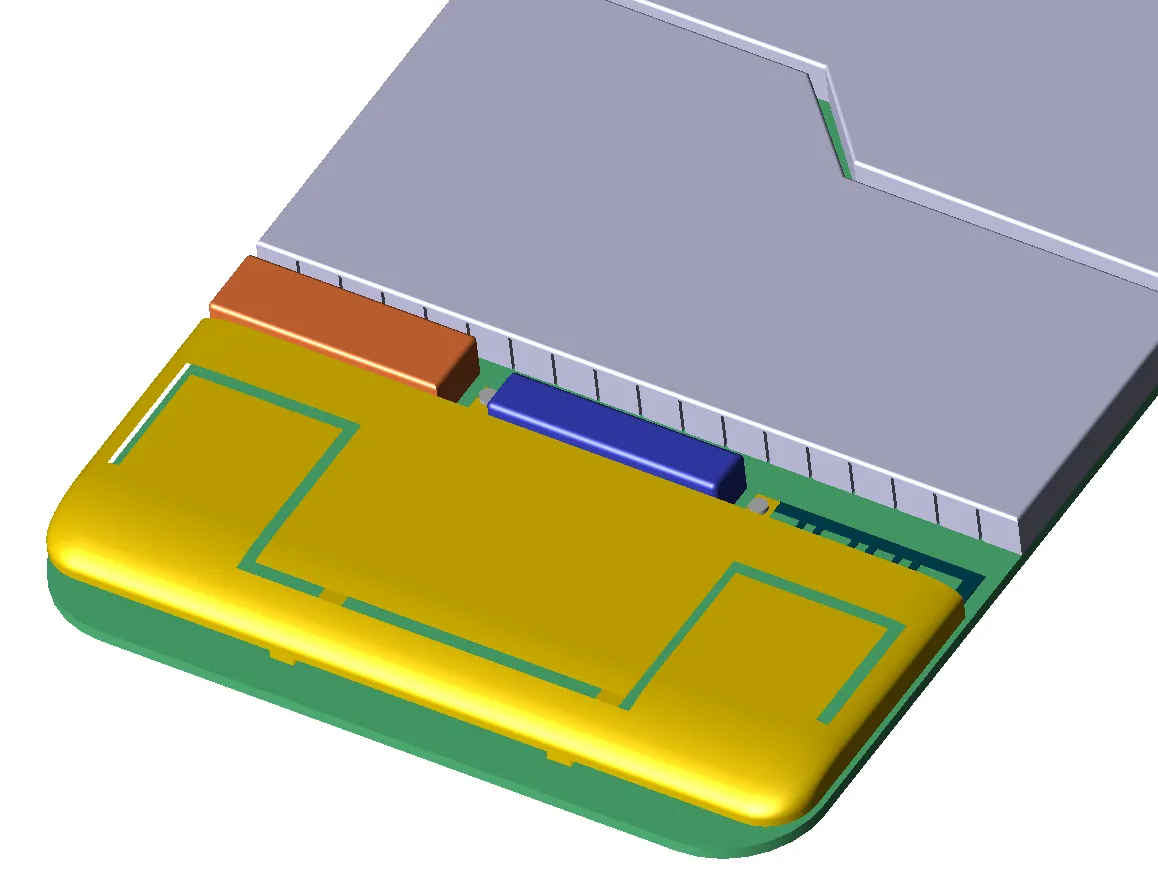
Figura 5: Malla conformada de antena de teléfono móvil.
Materiales
El software de simulación FDTD es capaz de simular una amplia variedad de materiales eléctricos y magnéticos. El material más básico es, por supuesto, el espacio libre. Todas las celdas FDTD se inicializan como espacio libre y los campos en todos los bordes de la celda se actualizan utilizando las ecuaciones del espacio libre, a menos que se añada otro material para sustituir el espacio libre.
Los materiales conductores eléctricos y magnéticos perfectos se simulan estableciendo el campo eléctrico o magnético en cero para cualquier borde de celda situado dentro de estos materiales. Debido a la simplicidad del cálculo para estos materiales, es mejor utilizar un conductor perfecto en lugar de un conductor real siempre que sea factible. Conductores como el cobre pueden simularse en FDTD, pero como las ecuaciones para calcular los campos en el material de cobre son más complicadas que las de un conductor perfecto, el cálculo llevará más tiempo. Por supuesto, para los casos en los que sólo un pequeño porcentaje de las celdas FDTD se definen como un conductor, la diferencia en el tiempo de ejecución apenas será perceptible.
Los materiales dieléctricos y magnéticos independientes de la frecuencia se definen por sus parámetros constitutivos de permitividad relativa y conductividad o tangente de pérdida para el material eléctrico, o permeabilidad relativa y conductividad magnética para el material magnético. En muchos casos, incluso cuando se realiza un cálculo de banda ancha, estos materiales son apropiados, ya que los parámetros no varían significativamente a lo largo de la gama de frecuencias.
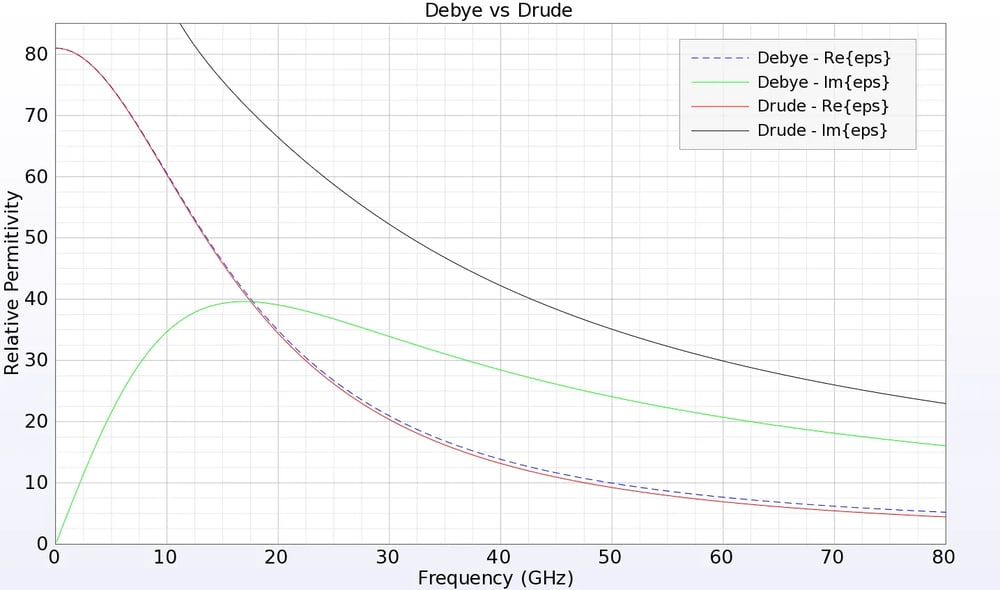
En algunos casos, un material independiente de la frecuencia no es adecuado y, en su lugar, debe sustituirse por un material dependiente de la frecuencia o dispersivo. Algunos ejemplos comunes de materiales dependientes de la frecuencia son los materiales con alto contenido en agua, como los tejidos humanos, los metales cuando se excitan a frecuencias ópticas y los dieléctricos en anchos de banda amplios. XFdtd incluye la capacidad de simular materiales eléctricos y magnéticos de Debye y Drude como plasmas, materiales de Lorentz y ferritas magnéticas anisotrópicas, así como dieléctricos anisotrópicos independientes de la frecuencia. Estos materiales pueden tener permitividades o permeabilidades negativas en algunas frecuencias, lo que los hace eficaces para simular metamateriales macroscópicamente. FDTD también es particularmente eficaz en la simulación de materiales no lineales, varios de los cuales están incluidos en XFdtd.
Zona cercana frente a zona lejana
Para cualquier cálculo, la geometría de la estructura que se simula se define fijando los bordes de las celdas en lugares específicos a determinados materiales. Todo el espacio geométrico FDTD, comúnmente llamado rejilla o malla, se compone de un bloque tridimensional de estas celdas. Este volumen tridimensional se considera la región cercana a la zona en FDTD en términos de almacenamiento de datos. El valor del campo en cualquier borde de la malla FDTD puede observarse en función del tiempo guardando un punto de "zona cercana" en XFdtd. También pueden almacenarse otros tipos de datos, como magnitudes de campo en estado estacionario, tasas de absorción específicas, parámetros S o impedancia para los puntos, superficies y volúmenes apropiados dentro de la malla.
Es posible crear una malla FDTD lo suficientemente grande como para permitir el muestreo de puntos en el campo lejano de una geometría. En general, esto será extremadamente costoso en términos de memoria del ordenador y tiempo de cálculo, ya que el número de incógnitas (celdas) será muy probablemente grande. Tenga en cuenta que cada celda FDTD tiene un tamaño máximo de una décima parte de una longitud de onda, por lo que alejarse muchas longitudes de onda de una estructura requerirá un gran número de celdas. En la mayoría de los casos, éste no es un método adecuado para controlar los resultados de campo lejano.
Un método más práctico para transformar los valores de campo a la zona lejana y para los cálculos de ganancia de radiación o patrones de dispersión de radar es utilizar una transformación para convertir los valores de la zona cercana en la malla FDTD en un valor de campo lejano en algún lugar alejado de la malla. Esto se hace encerrando la geometría en una caja y almacenando los campos en las caras exteriores de esta caja para problemas generales de zona lejana. Las caras de la caja están situadas a cinco celdas FDTD de cada borde exterior de la malla FDTD. Para que la transformación sea válida, todas las partes de la geometría FDTD deben estar contenidas dentro de la caja.
El sistema de coordenadas polares utilizado en XFdtd se define con el ángulo acimutal (phi) referenciado desde el eje x y el ángulo de elevación (theta) referenciado desde el eje z, como se muestra en la Figura 6. Este sistema de coordenadas se utiliza para localizar las posiciones de la zona lejana y para definir la dirección de la onda plana incidente. Este sistema de coordenadas se utiliza para localizar las posiciones de la zona lejana y para definir la dirección de la onda plana incidente.
.webp?width=269&height=254&name=image-asset%20(4).webp)
Figura 6: Sistema de coordenadas polares utilizado para la zona lejana y las direcciones de las ondas planas incidentes.
Cálculos de banda ancha y estado estacionario
Generalmente se realiza un cálculo de banda ancha con FDTD, ya que un único cálculo puede dar resultados para una amplia gama de frecuencias sin requerir recursos informáticos adicionales. Cuando se necesitan datos a determinadas frecuencias, los datos en estado estacionario pueden calcularse a partir del cálculo de banda ancha mediante una transformada de Fourier.
Ejemplos comunes de datos vs frecuencia incluyen patrones de antena en frecuencias específicas, aplicaciones biológicas como la Tasa de Absorción Específica (SAR), magnitudes de campo eléctrico y magnético, magnitudes de flujo magnético, corrientes de conducción, e información de tipo "circuito" como Parámetros-S, retardo de grupo, impedancia, potencia, eficiencia, etc.
La excitación sinusoidal puede ser deseable en ciertos casos ocasionales, como cuando se evita una resonancia fuerte cerca, pero fuera, de la gama de frecuencias de interés.
Límites exteriores de radiación
Una malla tridimensional de celdas forma la geometría FDTD y los campos actualizados en cada celda dependen de los campos vecinos. Sin embargo, debido a las limitaciones de memoria, la malla debe terminar en algún punto y, por ello, los campos de los bordes exteriores de la malla no pueden actualizarse correctamente. Para corregir esta situación, se aplican condiciones de contorno de radiación exterior en los bordes de la malla FDTD.
El límite exterior de radiación es un método para absorber los campos que se propagan desde la malla FDTD hacia el límite. Al absorber estos campos, la malla parece extenderse eternamente. El funcionamiento de los límites exteriores es un factor importante en la precisión de un cálculo FDTD y se debe tener cuidado para utilizarlos correctamente.
En algunos casos se prefiere una frontera reflectante a una absorbente. Puede utilizarse una frontera perfectamente conductora (eléctrica o magnética) para representar los campos en un cálculo FDTD y aprovechar las simetrías del problema. Una condición de contorno periódica es útil para simular una única celda unitaria de una gran geometría simétrica.
Recursos informáticos
FDTD es un método de cálculo intensivo y la mayoría de los cálculos razonables necesitarán un ordenador rápido y al menos unos Gigabytes de memoria. Para la mayoría de las aplicaciones es bastante sencillo estimar la cantidad de memoria necesaria para un cálculo. El factor más importante para el uso de memoria, y en gran parte el tiempo de ejecución, es el número de celdas FDTD utilizadas para representar la estructura bajo prueba. Cada celda FDTD tiene seis valores de campo asociados: tres campos eléctricos y tres campos magnéticos. Además, cada celda tiene seis banderas asociadas para indicar el tipo de material presente en cada una de las seis ubicaciones de campo. Los valores de campo son números reales de cuatro bytes cada uno, mientras que los indicadores pueden tener un byte cada uno. Esto supone un consumo de memoria por celda FDTD de 24 bytes para los campos y 6 bytes para las banderas, lo que da un total de 30 bytes. Para calcular la memoria total necesaria, en bytes, basta con multiplicar el número de celdas FDTD por el valor de 30 bytes por celda. El cálculo conlleva cierta sobrecarga, pero en general es bastante reducida. Una excepción notable son los ángulos de banda ancha de la zona lejana, que asignan seis matrices unidimensionales de valores reales por dirección.
Estimar el tiempo de ejecución de un cálculo FDTD es más complicado, ya que el rendimiento de los procesadores informáticos varía. Un método de estimación consiste en calcular el número total de operaciones que deben realizarse. Durante los cálculos FDTD se realizan unas 80 operaciones por celda y por paso de tiempo. El número total de operaciones se obtiene del producto del número de celdas, el número de pasos temporales y el factor de 80 operaciones por celda y paso temporal.
Si se conoce un valor del rendimiento en coma flotante del procesador, se puede calcular un valor para el tiempo de ejecución. Sin embargo, en general, un método de estimación mejor consiste en determinar el tiempo de ejecución de un problema sencillo en un ordenador determinado y, a continuación, escalar el tiempo por la relación del número de operaciones entre el cálculo deseado y el sencillo.
Hay muchas formas de aumentar la velocidad de cálculo de FDTD, aunque algunas requerirán un esfuerzo considerable de programación. Algunas de las más eficaces son utilizar varias CPU de un ordenador en paralelo, utilizar varios ordenadores en paralelo, optimizar los bucles de cálculo para la caché o aprovechar métodos paralelos en las CPU como SSE y AVX. El software FDTD es especialmente adecuado para el cálculo en procesadores GPU, ya que la noción de muchas celdas ejecutando un número relativamente pequeño de algoritmos de actualización en paralelo encaja bien con los métodos desarrollados para la actualización de pantallas de vídeo.
Referencias
-
C95.3.2002, "Recommended Practice for Measurements and Computations with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 100kHz to 300GHz", IEEE Standards and Coordinating Committee 28 on Non-Ionizing Radiation Hazards, abril de 2002.
-
K. S. Kunz y R. J. Luebbers, "The Finite Difference Time Domain Method for Electromagnetics", Boca Ratón, FL: CRC Press, 1993.

Seminarios en línea
Simulan el uso de satélites LEO para extender la cobertura NB-IoT a zonas rurales
En esta charla, Remcom presenta los resultados de un estudio que utiliza su software de simulación de trazado de rayos Wireless InSite® para predecir cómo podría complementarse la cobertura 5G terrestre con un enlace satelital LEO para mejorar la cobertura NB-IoT en zonas rurales.
Explore Recursos
Publicaciones
Novedades de XFdtd
La versión 7.11.1 de XFdtd introduce varias mejoras diseñadas para aumentar la precisión de la simulación, ampliar las capacidades de análisis y agilizar el flujo de trabajo de ingeniería. Esta versión refleja el enfoque continuo de Remcom en la resolución de retos de alto valor en el diseño de antenas, el modelado de PCB y el desarrollo de sistemas phased array.
Explore Resource
Seminarios en línea
Modelización y simulación de escenarios dinámicos de RF mediante movilidad basada en el tiempo
Conéctese para ver en profundidad el modelado de entornos dinámicos de radiofrecuencia con Wireless InSite, una potente plataforma de predicción y simulación inalámbrica. Los espectadores aprenderán a simular el movimiento de transceptores, antenas y objetos en escenarios definidos por el usuario, con aplicaciones que van desde los sistemas de comunicaciones terrestres a las misiones lunares.
Explore RecursosAhorre tiempo y reduzca costes.
Póngase en contacto con Remcom hoy mismo para obtener una solución personalizada a sus retos electromagnéticos más complejos.
Solicitar presupuesto